How fast can you throw Coldplay’s X&Y album?
(Because, you know, it’s an article about how fast sound can theoretically travel…and Coldplay has a song called “Speed of Sound”…and it’s on the X&Y album…I’ll stop now.)
ANYWAY.
So we all know about the speed of light, right? According to Einstein’s theory of special relativity, the fastest a wave can possibly travel is about 300,000 km/s: the speed of light. But what about sound? That is, is there an “upper limit” to the speed of a sound wave? Well, turns out there is.
In general, sound waves travel faster through solids faster than they do through gases or liquids. For example, sound travels through a diamond about 35 times faster than it does through air. That’s about as fast as sound can normally go. But how fast could it theoretically go?
Scientists at Queen Mary University and University of Cambridge theorized that the speed of sound should decrease with the mass of the atoms in a substance, meaning that sound should be fastest through solid hydrogen. They couldn’t actually physically test this, though, as hydrogen becomes a solid only under very, very high pressure (like +1 million atmospheres) that cannot be replicated on earth (yet). So they basically did a bunch of quantum mechanical calculations to see what the result should be and found that yes, the speed of sound in solid hydrogen is close to the theoretical limit of the speed of sound.
So that’s pretty cool!
UH OH
BOOM!
I think it’s so cool that so many of the stars that we can see may not even be there anymore. As the article states, since Betelgeuse is 642 light years from us, it could have done its supernova show that long ago and we would still be seeing it as “normal” in the sky.
That’s super wild.
Also, “The Armpit of Orion” would be a fantastic metal band name.
THIS IS FASCINATING AND BEAUTIFUL AND IT IS NOW MY DESKTOP WALLPAPER
Holy fucking shit.
What you’re seeing here are cell-like regions of the sun’s plasma that result from the turbulent motions of hot plasma rising to the surface of the sun, cooling, and sinking again. This process of convection affects the sun’s magnetic fields, which can lead to solar storms if the fields get tangled enough.
For perspective, note that each of those “cells” is about the size of Texas.
Isn’t this beautiful, though, seriously? I love it so much.
Let’s Talk About Sound
Or, more specifically, how to kill people with it!*
Sound, as we all know, is a physical thing. It comes from vibrations moving through matter (including air, of course). A sound begins when something causes a vibration. This vibration creates a longitudinal wave traveling through matter. This wave is actually a pressure wave. If said pressure wave hits our eardrums, then we hear a sound.
The volume or loudness of a sound is based on the amplitude of these vibration-created pressure waves. A loud sound will have a larger oscillation between the high and low pressures of the waves when compared to a soft sound, meaning that loud sounds have higher high pressure sections and lower low pressure sections than soft sounds.
This is kind of convenient because it allows there to be a threshold for what we can consider to be the “loudest” sound—if the low pressure gets too low, it hits vacuum-level and cannot go lower. So the loudest sound is something that creates low pressure sections between waves that are nearly vacuums.
(Wild.)
In fact, what we consider to be the “threshold of sound” on the loud side of the scale (at least on earth) occurs at 194 decibels.** And where do we hit the point where sound can be deadly? Somewhere around 185-200 decibels.
Here are a few good resources/articles that talk about sound in general as well as what happens when you start approaching (or passing!) that “here is where sound gets deadly” threshold.
It’s actually kind of disturbing to think about. But also really cool.
*Sound killing people was actually something I focused on in my 2012 NaNoWriMo, “Whistler’s Father.” A scientist and an artist were working together to create the “perfect” sound—something that would boost mood, health, and would overall make people “better” if they were to hear it. But it turned out that the perfect sound was actually deadly if it was listened to for too long; the scientist in my story ends up killing himself via this perfect sound because he becomes addicted to it and is unable to stop listening to it in time to prevent his own death. Yeah, that was a cheery NaNo.
**You can get sounds louder than this, but the vibrations that create them don’t create waves (again, because of that low pressure threshold) but they still create something. Things like the atomic bombs dropped on Japan and the eruption of Krakatoa, for example, were louder than 194 decibels, and were very destructive if we even just consider the sounds (or rather, the spikes in atmospheric pressure) they produced.
The Matter of the Heart
So here’s an interesting article.
It talks about a study that focused on comparing the hearts of chimps, gorillas, and humans (classed as one of the following: endurance athletes, football linemen, farmers, and inactive people). The researchers wanted to look further into human’s rather unique endurance ability – our ability to run/walk long distances.
For the gorillas and chimps, they spend a lot of time sleeping or just generally being inactive and have occasional quick bursts of energy and stress (such as quickly climbing trees or fighting). The researchers believed that these quick bursts caused spikes in blood pressure, but found that the shape of the gorilla and chimp hearts were suited well for these spikes. The hearts were round and had thick walls.
The human heart is different. It is larger than chimps’ hearts and less thick and also twists/rotates when it pumps blood (the gorilla and chimp hearts don’t). This allows for a more efficient blood delivery system and is ideal for endurance activities. The trade-off, though, is that the walls of the human heart aren’t as thick and thus are not as well-built for sudden blood pressure spikes.
Another interesting finding from the research is that if a person tends to live a sedentary life, their heart will “remodel” itself and become more like a chimp heart: less flexible with thicker walls. These hearts also appear to look like the hearts of people with chronic high blood pressure even before high blood pressure actually sets in.
They use this finding to emphasize the importance of regular exercise, noting that previous research showed that hunter-gatherers (in certain areas) tended to walk somewhere between six and nine miles a day. Physical activity, as we’ve all been told, is key to maintaining the flexibility and durability of the human heart.
ZOMG MEASURES
Holy crapples, guys, so you know how I was talking about the kilogram (again) the other day?
I HAVE FOUND THE JOURNAL TO END ALL JOURNALS
Metrologia is a journal about the scientific aspects of measurement – most commonly those involving the seven base SI units.
Here’s an article talking about the kilogram.
I will disappear into this journal forever now, bye.
Kilogram? More like COOL-ogram…right?
So once again, while Nate and I were playing an old Jeopardy game, the topic of the kilogram came up (there was a “Weights and Measures” category, so I’m not totally to blame this time). I was blabbing on about Le Grand K, the physical kilogram (THE kilogram…at least until it was redefined) and said something to the effect of “I guess they’re not going to be using that anymore…I want it!”
Like, can you even imagine sending an email to the International Bureau of Weights and Measures that read something like:
To Whom It May Concern,
So I just heard the big news that the kilogram is now defined based in part on the Planck constant, rendering the International Prototype of the Kilogram obsolete.
Now I’m just some pleb, but here me out: if y’all aren’t using the IPK anymore, I’d be happy to take it off your hands. I’ve got a nice space for it on my trinket shelf, and it would help de-clutter things for you now that the kilogram is no longer technically defined by an artifact.
Anyway, think about it. I can pay for the shipping costs, too, if that would sway your decision!
Thank you for your time,
Claudia
The idea of some random person just emailing the Bureau of Weights and Measures to ask if they could have the IPK is absolutely hilarious to me.
‘Cause I have that kind of dumb sense of humor.
That’s Why They Call Me Mr. Fahrenheit
I really like this explanation of why Fahrenheit is a good “understandable” temperature scale, even though its set points of 0 and 100 are kinda wonky. It’s practical and intuitive for human “day-to-day” use. It’s also more precise.
I love me a kilogram, but I’ll be damned if I ever support Celsius.
(And yes, I know I take this stuff way too seriously.)
Curvalicious
Let’s look at the super cool ISOCHRONOUS CURVE!
This video does a good job of demonstrating that the periodic motion of an object on a (frictionless) isochronous curve has a period that is independent of where the object starts on the curve. It’s a pretty cool little thing.
Edit: OH MY GOD, A WHOLE WEBSITE ABOUT CURVES AND SHAPES
(I’m going to link to one of the pages, ‘cause it looks like the majority of the site is in French, but some of it has been translated to English. I’ve clicked through a lot of the curves using the links at the bottom and I’ve only hit English pages, so if you want to look at some curves, that might be the best way to go (unless you know French)).
LAMINAR FLOW
This guy’s absolute adoration of laminar flow is so freaking awesome.
Is…is this how I am with Leibniz?
Absolute Unit(s)
This makes me abnormally excited. I don’t know what it is with me and the SI units, but I dig ‘em, man.
And let’s be honest: I searched “kilogram” and read every related bit of info that came up, ‘cause the kilogram is my bro.
WANNA LEARN ABOUT PUPILS?
Basically, pupil shape is at least somewhat tied to whether an animal is more of a (grazing) prey animal or more of a predator. The article talks a lot about goats and sheep, and goats and sheep are pretty cool, so if you’re not into pupils, maybe you’re into goats and sheep.
(Sorry, I haven’t slept in like three days)
Spaaaaaaace!
I love this guy’s video simulations of space stuff.
I also love the disclaimer “Saturns rotation is extra impossible, but I had to prevent the rings from colliding.”
Don’t we all, yeti dynamics? Don’t we all?
*screeches in metric*
So y’all know I love the SI units, right? Hell, the “kilogram” tag on this blog is used frequently enough that it shows up in the “Tags” list on my front page.
Well, another closely-related thing I love are the SI prefixes. These are things like kilo or nano or yocto (which got its own blog a while back) that precede a unit and indicate either a multiple (like “kilo” suggests a thousand times something) or a fraction (like “milli” suggests a millionth of something) of the unit. Kilogram, nanosecond, millimeter, etc.
That kinda stuff.
Well, I guess four new prefixes have been proposed for the next levels of super big and super small: ronna and ronto for 1027 and 10-27 respectively, and quecca and quento for 1030 and 10-30, respectively. If they’re approved, they’re set to be officially put into place in 2022, making them the first prefixes approved since 1991.
And that is way too cool.
(I love the prefixes and I’m not sorry.)
TIL: The Planck Constant can be hilarious
Alternate title: GOD I’M OBNOXIOUS
Hokay. So Nate and I were playing Jeopardy this evening and some question* came up that made me think of the kilogram. This got me ranting and raving about said kilogram, as I am wont to do, so I looked it up on my phone because I knew that there have been recent attempts to redefine the kilogram based on a physical constant and I wanted to see exactly what that redefinition would be.
This eventually led to looking up the Planck constant, which led to viewing this equation:
Of course it’s the mobile version of Wiki so it scrolls right in order for you to view the rest of the equation, but I initially didn’t think of that and I thought it was beyond hilarious that the Planck constant equaled 4.1. 4.1 what? Who the hell knows, that’s why it was funny.
Anyway.
*I can’t recall the specifics of the question, because like any well-adjusted happy person, I gloss over large amounts of my existence so that it’ll feel like I reach death faster.
CC
Remember that bomb blast simulation I mentioned a few days ago? They have an interactive “how will climate change affect you?” map as well.
Scary stuff.
Solar FAIL!
Huh. Interesting.
Are you Koppen with your climate?
So this is a cool little website. It lets you type in a city and highlights places around the world that have similar climates to that city.
Here’s Calgary, with its Dfb Koppen climate (continental climate, no dry season, warm summer)
Moscow, with its Csb Koppen (middle latitude climate, dry season in a warm summer)
Vancouver, with its Cfb Koppen (middle latitude climate, hell on earth no dry season, warm summer)
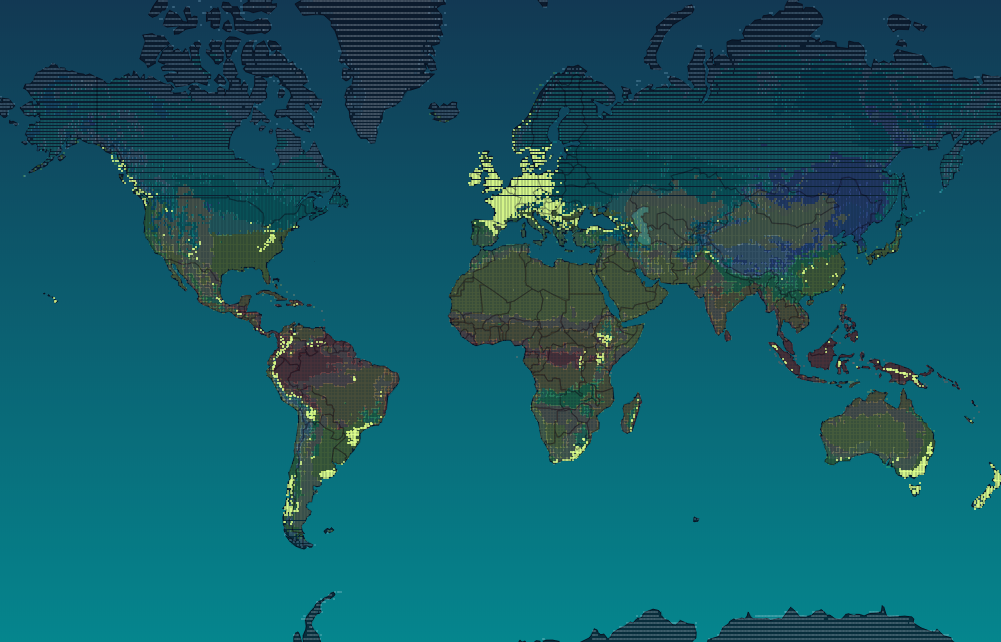
And Tucson, with its BSh Koppen (dry and hot semi-arid climate)
Nice!
ZOOM
Have you ever seen a canopy like this?
(Picture from here)
What’s going on with those gaps between the leaves/branches? Turns out there’s this thing called “crown shyness,” a phenomenon observed in some species of trees. The phenomenon occurs when different trees’ crowns do not touch each other, leaving these funky channels of gaps between the crowns.
No one really knows what causes this crown shyness. One theory is that the behavior is adaptive, helping to prevent the spread of bugs/larvae that eat leaves. Another theory is that the behavior develops due to the fact that too-close branches can be damaged in storms and high winds from bonking into one another. Still another theory has to do with light. The behavior develops to help ensure that the leaves of a tree are not blocked by the shade of another tree’s leaves, thus getting an optimal chance for light.
Cool huh?
TWSB: More on the Kilogram
So I have no idea how I’ve never found this podcast before since it’s about the kilogram, but I haven’t.
But now I have.
Enjoy.
(Hot damn, I love the kilogram.)
This Week’s (Month’s?) Science Blog: Sun Block
Yo.
So as you all know, I find the sun to be very awesome. Here’s a video of a guy demonstrating that despite the fact that the sun seems so huge in our sky a lot of the time, that hugeness is an illusion! The sun is, in fact, only about half a degree in size in our sky.
Supah cool.
TWSB: Hey, A Science Blog!
Hey you butt parties, check this out: a study published in the journal Chemical Senses suggests that there may be a sixth taste in addition to the five basic ones we all know (sweet, sour, salty, bitter, umami). What taste is it? Starch.
The study, run by Dr. Juyun Lim from OSU, involved approximately 100 participants across five different studies. The participants were asked to taste liquid solutions of carbohydrates—some simple (like sugar) and some complex—both under normal conditions and when the sweet receptors in their mouths were blocked. Even with the receptors blocked, the participants stated that they could still detect a starchy taste, which goes against previous assumptions that starch was tasteless.
Dr. Lim says that the result is not necessarily surprising; since humans use starch as a major source of energy, it makes sense that humans could be able to detect its presence by taste. If nothing else, the findings demonstrate that the way humans taste is actually more complex than previously thought. The way the participants tasted the starch, says Dr. Lim, was by tasting the saliva-destroyed version of the starch: glucose oligomers. While it was previously suggested that humans could only taste the simple sugars class of carbohydrates, the fact that participants could actually describe the taste of the glucose oligomers suggests that our tasting of carbs is more complicated than we think.
Others are a bit wary of classifying this as a new separate taste, suggesting that it might just be another “version” of the sweet taste. More research will be done on determining the exact mechanism of how the glucose oligomers are actually tasted.
Yikes
Dudes. This is simultaneously the coolest and creepiest thing I’ve seen in a while. Basically, Graham is a person constructed to survive a car accident, either as a passenger or as a pedestrian. His head/brain/skull, neck, chest, skin, knees, and feet have all been adjusted to be optimally protected in an accident. It’s really interesting to read the reasons behind the changes.
Eigenblogger 