!
DID YOU KNOW THAT THERE’S A SUPER FACTORIAL?! I DIDN’T!
Recall the regular factorial: 6 factorial (6!), for example, is 6 x 5 x 4 x 3 x 2 x 1.
The super factorial of six, on the other hand, is sf(6) = 6! x 5! x 4! x 3! x 2! x 1!
On a related note, Wikipedia’s “Large numbers” article is quite fascinating. I love how when we start dealing with the absurdly large or absurdly small (and things related to them) our terminology gets really strange.
…
Okay, so I had a bunch of examples but then Word crashed and then Tumblr happened so you get this instead:
Math-inclined friends, I need your help!
So we’re doing trigonometric integrals in calculus and one of our homework problems is this little dude:
We rushed through this section of the chapter this morning ’cause we’re behind schedule and I’m a little shaky on them (also I’m dumb), so I went to the calc room in Polya to get some help. I showed one of the tutors in there this integral.
I told him how I thought we should start: since (1-cos2x) is the numerator of the half-angle formula for sin2x, we could multiply both sides of the half-angle formula to change (1-cos2x) to 2sin2x and then go from there.
He said he’d never even thought about solving it like that, but when I asked him what the “normal” method would be for this integral, he didn’t know.
So is there another way of solving this?
L’Hopitaaaaaaaaaal
One of our homework problems was to solve one of the examples that l’Hopital used in his original calculus textbook.
It took me a bit to figure it out ’cause I’m dumb, but after I finished it I actually wanted to find the original example in the original work. Surprisingly, it didn’t take too long to find. INTERNET POWERZ!
L’Hopital was French. His textbook is, therefore, obviously in French. Curse my unilingualism! I understand the numbers, though, haha.
How cool is it that we got to do this example? Seriously. I really, really hope they offer History of Mathematics class next fall.
Haha. Again, apologies for all the math-related blogs lately. But in all honesty, my life is about 60% math, 15% computer science, and 25% teaching statistics right now. A portion of one of those percentages will yield to some writing in a bit, but for now this is how it is.
If I’m annoying you, just ignore me for the rest of the semester.
Why explaining the Binomial Theorem to a fellow student is a big deal (to me)
Today I explained the Binomial Theorem to another dude in my discrete math class.
“Who cares?” You’re probably saying.
Well, let me tell you a little story.
I used to be good at math. Like, when I was a kid. In elementary school I was one of three kids who were in “advanced math” (we sat in a broom closet and did math out of junior high textbooks. We also gave each other really dorky math nicknames, but I can’t remember mine).
I wasn’t bad through Junior High, either. The only difference was that I’d hit the “who gives a crap about school” phase of my life, so I didn’t really try very hard.
But then I took Algebra II. And I had the worst teacher ever. He was the track coach, so he was really only teaching so he could stay the track coach. He’d stand in front of the class for about 10 minutes, write out a bunch of equations and graphs without explaining them (seriously), then go back to his desk and review track film for the rest of the period. We were to spend the rest of the time doing a bunch of questions from the book, and he would get visibly irritated if we came up to him to ask questions.
I’m not even kidding.
What’s worse is how stupid he made us all feel when we did ask questions. And algebra’s never been my strength anyway (geometry and calc FTW), so you can imagine the number of berating comments I got because I always had questions. And me being me, I associated the “you’re so stupid” feeling with math, and that quickly turned into “you can’t do math you idiot.”
I’ll spare you all the crappy details, but by about January that year I would literally break out in hives whenever I walked down the math wing of the high school. I managed to stick it out, though, and ended up with like a 69.97%, which turned out as a C minus on my report card. And if you know me, you know that’s HORRIBLE. Even in my “I don’t give a crap about school” phase I didn’t get C minuses in any of my other classes.
The “Claudia’s too dumb to do math” attitude lasted into college as I took Math 143 in fall 2006 (though I submit that class was just a horrible class in general) and had like 40 panic attacks over Math 160 (“Survey of Calculus,” kind of an abridged version of calc I with a lot less integration) in fall 2007. I didn’t hate math—I appreciated everything it gave us and the amazing applications—I just hated doing it. (Which is actually kind of funny, because I NEVER felt like that when I started taking statistics. But I see stats and math as very different topics. But that’s another topic for another blog, so moving on…)
Once I got far enough along in the field of stats, I obviously started doing things that involved a lot more advanced math than anything I’d ever dealt with before (e.g., calculating eigenvalues and eigenvectors in factor analysis). And I think at some point I realized that if I was ever going to get anywhere in stats, I might as well stop being an idiot, face my fear of not being good at math (yes, it’s a fear of not being good at math, not a fear of math), and take some freaking math classes
And so that’s my life right now.
Every once and awhile, especially if I see a problem that I have no idea how to solve, I still get this incredibly visceral feeling of fear and dread and despair and self-hatred over being too stupid to do anything of worth, but I try to fight it and stay calm (well, calm for me).
But yeah. I’m absolutely loving my math classes and I’m really excited to get to Math 451 and 452, the two “Mathematical Statistics” classes, because I’m anticipating some big “click” where the two subjects merge into some beautiful orgy of integrals and probability distributions (and when that happens, good luck seeing a blog about anything else).
Anyway.
I just thought I’d explain that a little bit and give you a reason why you’re seeing a lot of “Claudia spazzes about math” posts.
Dear Calculus II:
What right do you have to be so damn awesome?
L’Hopital’s rule* just made my day. It is the COOLEST FREAKING THING, man!
All of my readers who have had more advanced math are probably thinking “holy freaking crap, Claudia, shut UP with this fascination with all these things everybody else already knows,” to which I say, “NEVER! This stuff is beautiful and powerful and wondrous and gives me tinglies and should give you tinglies as well because IT ALL WORKS TOGETHER AND IT’S MIND-BLOWING HOW THE UNIVERSE FUNCTIONS SO SMOOTHLY WHEN THERE’S SO DAMN MUCH OF IT!”
Also, how in the hell can anyone fall asleep in Discrete Math? Multinomial Theorem = one sexy mofo. But I still suck at permutations/combinations. You’d think with all the stats stuff that such things would be somewhat intuitive to me now, but no.
Okay, enough blogging. Gotta get back to CALC!
*Actually, the rule was most likely developed by Johann Bernoulli; he had tutored L’Hopital and L’Hopital published the rule in his own textbook in 1696 under his own name (though he noted his debt to Bernoulli in the preface). This ticked Bernoulli off and there are letters he sent to Leibniz in which he complained about L’Hopital publishing the rule without proper acknowledgement. Sigh. Calculus, man.
Edit: woah, L’Hopital died on my birthday in 1704 and Bernoulli died on my grandpa’s birthday in 1748. Freaky.
CONTROL YOURSELF, CLAUDIA
(warning: caps lock abuse ahead. Ready yourselves.)
I should have learned by now that rants about my passions do not a ten page essay make.
Hell, it’s not even a rant. It’s just a history.
But it’s the calculus controversy! HOW CAN I NOT BE EXCITED?!
Seriously, this stuff is fascinating. Even if I didn’t have a massive lady boner for Leibniz, I’d be just as engrossed in this.
Newton was 23 years old when he came up with his method of fluxions and fluents.
TWENTY THREE YEARS OLD.
Can you imagine that? God, when I was twenty three I was busy binge-drinking Red Bull and trying not to spontaneously combust over my pittance of a Master’s thesis (“durrrr, what’s an eigenvalue?”). This guy was INVENTING CALCULUS.
And Leibniz taught himself Latin and was proficient in it by the time he was twelve. TWELVE. I couldn’t even count to ten in another language when I was twelve! He published his first book on combinatorics when he was twenty, even before starting his studies in math.
Freaking salfjalsfhfhsfahghghghh.
I love this stuff, but reading about it also makes me feel like an IDIOT, because what the hell have I done with my life?
But that is immaterial.
And the actual battle over priority between these two guys? Oh my god.
For a dispute over something as magnificent as calculus between two of the greatest minds ever, there was sure a lot of hair-pulling (wig-pulling?) and name-calling going on.
And it TOTALLY wasn’t a fair fight, either! Both men were members of the Royal Society of London. At the nastiest point of their fighting, Newton had been appointed President. He used his power to get a “report” he’d written on his own published as if it were an effort of the entire Society. The report basically said that Leibniz did, in fact, “have prior knowledge” of Newton’s calculus when he started working on his own. It was enough evidence against Leibniz to put him in a bad light for the rest of his life. He had one person attend his funeral when he died in 1716. Yup, the guy who co-invented calculus, the guy who refined the binary system, the guy who anticipated the distinction between the conscious and unconscious long before anyone else, had one person attend his funeral.
I mean, seriously. Isn’t that just sad? Don’t you feel badly for him? He deserved better, man.
Bah.
I’m like beyond hyper excited right now for some reason. Gonna go write some more of this essay, then gonna go work on NaNoWriMo nonsense. Haha, I’ve been pretty quiet about it thus far (shocking!) but that’s because a) it’s not as good of a plot as my previous three were, even though it’s coming along quite smoothly and b) school and teaching have so absorbed my soul that I even keep forgetting to update my word count on the website.
Maybe I’ll put up an excerpt later this month.
HUTTAH!
I used to think triangles without a right angle were “wrong triangles”
I’m digging this trig class. It’s only one credit, but I’m really enjoying it. It’s pretty sad that I avoided all math in high school after Algebra II just because of one horrible, horrible math teacher, but considering I used to break out in hives when I walked down the math wing of the building, I don’t know if trig and calc would have been possible for me back then.
Anyway.
I like to think the six trig functions each have their own personalities.
Sine is the smart one. He’s quiet and clever and knows the secrets of the universe.
Cosine is an average kind of dude, but somehow is incredibly lucky and is almost as knowledgeable as Sine just because they hang out with each other.
Tangent is like the quiet, gentle mother figure of the functions.
Cosecant is the super-socially-connected function. He’s the no-nonsense business type who likes to get things done.
Secant is a jerk. He’s super jealous of Cosine and is bitter that his own derivative involves Tangent.
Cotangent is somewhat misanthropic and resents being the inverse of Tangent. He’s not very fun. Even his derivative is a square (HA!).
Yes, this is what goes on in my brain.
Benford’s Law? More like Benford’s LOL
Okay, today’s going to be a quick little blog ‘cause I’m busy trying to organize/transfer/protect from any possible massive hard drive failures my music library. It’s stressing me out.
While I was working on the “References” section of a textbook today at work, I noticed a pattern that I’ve come in contact with several times: there appeared to be a lot more “entries” that started with a letter from the first half of the alphabet (A – M) rather than the latter half (N – Z). I’ve done at least one other analysis regarding this topic, but I decided to do another slightly different one to see if it applied in this case.
QUESTION OF INTEREST
So what is Benford’s Law? For those of you who don’t want to click the link (lazy fools!), Benford’s Law states that with most types of data, the leading digit is a 1 almost one-third of the time, with that probability decreasing as the digit (from 1 to 9) increases. That is, rather than the probability of being a leading digit being equal for each number 1 through 9, the probabilities range from about 30% (for a 1) to about a 4% (for a 9).
What I want to see is this: is there a “Benford’s Law” type phenomenon for the letters of the alphabet? That is, do letters in the first half of the alphabet appear as the first letter of words more often than letters in the latter half of the alphabet?
HYPOTHESIS
In a given set of random words, a greater number of words will start with a letter between A and M than with a letter between N and Z.
METHOD
Using this awesome little utility, I generated (approximately) 5,000 words each from The Bible, Great Expectations, and The Hitchhiker’s Guide to the Galaxy. I then counted how many words there were starting with A, how many words there were starting with B, and so on for each letter of the alphabet.
I then did two other breakdowns of the letters:
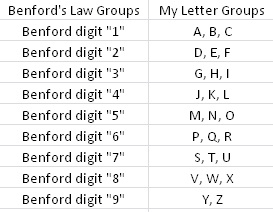
A) I divided the alphabet in half (A – M and N – Z) and counted the total number of words for each group.
B) In order to “mirror” a sort of Benford’s Law type of structure, I divided the 26 letters into nine groups (eight groups of three letters each, one group of two letters). I wanted to make a similar breakdown of groups to the nine numbers that Benford’s Law applies to, just to see if that sort of arbitrary screwing around did anything. Visualization ‘cause I suck at explaining stuff when I’m in a hurry:
Kay? Kay.
RESULTS
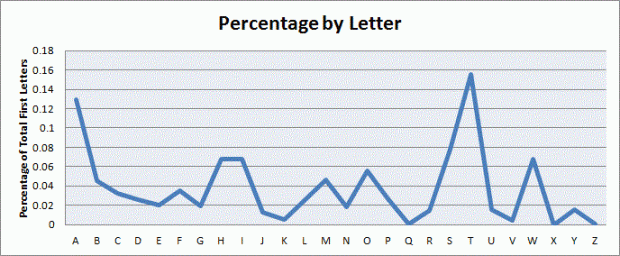
I made charts!
By “half of the alphabet” in what is probably the most worthless visual ever:

By semi-arbitrary group (dark blue) with Benford’s percentages by number (light blue) for comparison:

DISCUSSION
Well, that whole thing sucked. Okay, so obviously it’s not a perfect pattern match and I didn’t do any stats (I WAS IN A HURRY) to see whether there was any statistical significance or anything, but it was fun to screw around with for an hour or so. I wonder how different the results would be (if at all) if I were to use truly random words from the English language, not just random words selected out of three works of fiction. Perhaps material for a later blog…?
END!
Cake is a Lie, Pi is a Constant
Oh look, it’s Pi Day.
Have you heard, then, of Tau Day?
“The true circle constant is the ratio of a circle’s circumference to its radius, not to its diameter. This number, called τ (tau, is equal to 2π, so π is 1/2τ—and March 14 is thus Half Tau Day. (Of course, June 28, or 6/28, is Tau Day itself.) Although it is of great historical importance, the mathematical significance of π is simply that it is one-half τ.”
http://www.math.utah.edu/~palais/pi.pdf
Interesting notion. Canadian news websites: reporting the slightly quirky version of Pi Day for all of us to enjoy.
Math Puns: The First Sine of Madness
I’ve been in a math mood as of late. Here are some things that are fun.
– Create an arbitrary matrix. See if you can find the eigenvalues.
– Do stuff like this. Or just mathify food in general (Tukey sandwiches! Chocolate chi-squares! Mandelbratwurst! The ever punnalicious pumpkin pi! I could go on…). I think if we all had to Fourier transform our breakfasts in the morning our lives would be a lot cooler.
– I do interval workouts on the elliptical machine in the rec center. During the high intensity intervals, I start at zero in my head, count up to the next prime number, and count backwards to zero. Then I start again, counting up to the prime number after the first prime number, count backwards to zero, and repeat ad nauseum (like this: 0,1,0; 0,1,2,1,0; 0,1,2,3,2,1,0; 0,1,2,3,5,3,2,1,0; etc.).
– Do stuff like Zeno. Whenever you have to do something for a set period of time (like 30 minutes), divide the time in half in your head then, when you reach the halfway time, divide it in half again, and again, and again, until you’ve got like a minute left. I find this helps the time pass more quickly when I’m doing something not so enjoyable. Plus it’s fun.
– This video:
Yay!
Today’s song: Rich Girl$ by Down With Webster
Calculus can solve many problems, BUT CAN IT FIND YOUR GOD?!
There are few things weirder than math, I think. It’s systematic, but it’s also really creepy.
Take calculus. Given some curve y = f(x) for some equation x, you’re able to find the slope of the tangent line to that curve at any given point just by finding the derivative f’(x). How do you find the derivative? There are like five main rules you need to know to be able to find it for any equation x (ignoring e and all that crazy natural log stuff for now).
I know I’ve blogged about this before, but does anyone else find that incredibly…convenient? The fact that many mathematical problems can be reduced, in some form or another, to addition, multiplication, subtraction, and division is kind of frightening.
And the fact that nearly all problems we’ve come across have some sort of mathematical explanation to them—and not only a mathematical explanation, but a mathematical explanation that works with the way we’ve defined mathematics on this little planet hurtling through space, this infinitesimally small rock in the whole expanse of the universe? Insanity!
It freaks me out that we’re able to explain things like space phenomena using our math. I’m probably just a simpleton, but it freaks me out. How has (nearly) everything we’ve found conformed to our little system of manipulating numbers? How is it that the formulae and procedures we’ve developed coincide so nicely with the workings of what we’ve seen of the universe? I really don’t know what to think of it anymore. As I’ve said, I think if there were any plausible explanation for a god, it would lie in math.
But what do I know?
Today’s song: Luna by Evgenij Anegin
I am deriving so much pleasure from calculus that I may need to integrate it into my daily life
HOT DAMN I love calculus.
And no, it’s not just because the great and glorious Leibniz invented it, either. It’s very methodical and I actually know what the hell I’m doing (for most of it). I think I hated it so much the first time around because it was at 8:30 in the freaking morning AND because it was all business-oriented. And because I didn’t really care back then. I dig the tediousness of it all—it’s less tedious than eigenvalues (thank god) but still fun. It feels weird to be doing a metric crap ton of math homework again.
Oh, and THERE’S A FREAKING ICE CREAM TRUCK OVER HERE, TOO! Totally not an imaginary one, either…I saw it go down 43rd street blasting out a lullaby.
I’m not insane. Bad ass.
Today’s song: Glycerine by Bush
Further Proof of Google’s Evil Grasp on the Universe
LINEAR ALGEBRA IS BEHIND IT ALL!!
As much as I hated finding eigenvalues and eigenvectors (which was a lot), this article’s actually very interesting. Probably because some of this stuff is relevant to factor analysis, which is sexiness in statistics form.
That is all.
Today’s song: Animal by Miike Snow
Wiggity Wiggity Wiggity BLOG
I FREAKING LOVE this stuff. Especially since patterns like this were big parts of my NaNo.
Yay. :)
I HAVE THE URGE…
THE URGE TO UNDERSTAND MATH!
I don’t know what it is about this subject. It terrifies the hell out of me (especially when I have to take a class in it), but yet when I don’t understand something about it I have this incredible urge to take as many math classes as my soul will allow me in order to actually “get it.”
Right now I want to take calculus again. Lots of it. Mainly because I forgot all that I learned due to losing my notes and the class being at 8:30 in the morning (whose brilliant idea was that, anyway?).
Sigh.
I guess I’m realizing that now that I’ve started grad school, I’m one major step closer to pigeon-holing my education. It’s not undergrad anymore, where nobody gave a crap what I took. I actually have to “stay on task.” Which is surprisingly difficult for me.
Whatever.
Deconstructing Pi
Today I did something fun (and something that crashed SAS at least 10 times): I decided to deconstruct pi to the 1 millionth digit. Why? I wanted to see if the numbers 0-9 appeared nearly uniformly throughout this fraction of such an infinitely long number. I wanted to test the hypothesis that a large enough sample size with the instances seemingly “random” would produce a much less leptokurtic (bell curve-shaped) distribution.
I also like the word “pi.”
STEP BY STEP PROCESS!
First I went here to get the first million digits.
Then I used the handy-dandy CTRL-H “find and replace” command to put spaces behind each digit so that SAS could read each one as a distinct piece of datum.
So after SAS crashing on me like 4 billion times (it took awhile to be able to input the most amount of data but not have it flip out—no seriously, this took like three hours), I finally got all the data into SAS and analyzed it. Here are codes/output!

As you all know, the mean of numbers 0-9 is 4.5. When n=1,000,000,the mean of all this data is 4.499934, about as close to 4.5 as you can get. And there’s practically no skewness, either.
Here’s the bar chart:

And, appropriately, here’s the pie chart:
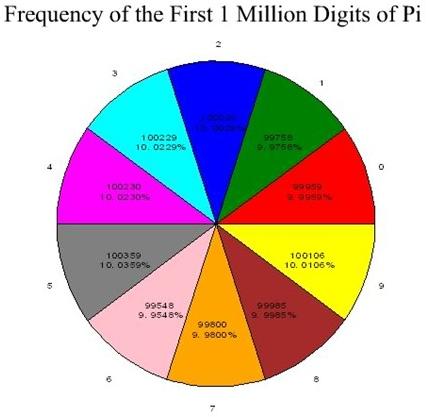
How freaking GORGEOUS is that uniformity?! I mean, LOOK at it!
Breakdown by smallest to largest frequency:
6: 99,548
1: 99,758
7: 99,800
0: 99,959
8: 99,985
2: 100,026
9: 100,106
3: 100,229
4: 100,230 (ONE instance difference between digits 3 and 4! OMG!)
5: 100,359
The power of the large sample size, my friend. Cherish it. Admire it. Worship it.
I’m done here.
Alliteration’s Almost Always Appropriate
I’m sorry, but I must address this issue, as I had a dream about it mere hours ago (it’s like 10 AM) and if it’s infiltrated my dreams, it must be important to me.
So as I’ve stated, I’m reading The Calculus Wars. In the blog about said book, I briefly mentioned the fact that the book used the word “invented” to describe how calculus came about. As I read on, though, the author appears to switch randomly between the words “invented” and “discovered.”
As confused as I was at the beginning over this, I’m more confused now, mainly because I’m not sure which word should really be used. Really, what sounds more accurate?
If we say that Newton and Leibniz discovered calculus, that basically means that there is some sort of preexisting system of mathematics that humans are in the process of unlocking.
But if we say that they invented calculus, then it just seems kind of strange that they were able to just invent something with such mathematical power to explain all the things it explains.
But then again, I find it rather suspicious that human beings have developed these systems called “numbers” and “math” and they somehow magically explain the workings of the universe (velocity, the speed of light, rate of acceleration, etc.). I mean, don’t you find it the least bit suspicious that we can explain these things using simple formulas? It makes sense that the universe is ordered in some fashion, I just find it kind of odd that we’ve managed to gain possession of something that seems to be able to explain the patterns. It seems too easy, you know what I’m saying?
What if it’s all arbitrary?
(See, this is why I want to take freaking Metaphysics)