Are You There, God? It’s Me, Non-Normality
I’m here to talk to you today about nonparametric statistics. What are nonparametric statistics, you ask? Well, they’re a collection of statistical tests/procedures that we can use when data do not satisfy the assumptions that need to be met in order for conventional tests/procedures to be carried out. For example, suppose Test A requires that the data are normally distributed. You gather data of interest and find that they are not normally distributed. Thus, Test A should not be used because its results might be inaccurate or maybe even uninterpretable with these non-normal data. Instead, you must use a test for which normality is not a requirement. If such a test exists—say, maybe it’s Test B—then Test B may be considered a nonparametric test. It can be used in place of Test A if Test A’s assumptions are not met. Cool, huh?
Let’s look at a few examples, because I haven’t pressed any statistics on you guys in a while.
Example 1: Comparing Different Treatments
Scenario: You are a plant scientist. You have a specific type of plant and you want to see to what extent lighting affects this plant’s growth. You have three lighting conditions: sunlight, fluorescent light, and red light. Basically, you want to see if there is a significant difference in the amount of growth for plants grown in these three different conditions.
Parametric test: Analysis of variance (ANOVA) seems appropriate here; you can basically assess the differences in growth by comparing the mean growths for each of the three conditions.
Nonparametric test: For ANOVA to be accurate at all, the data need to be normally distributed. Suppose your data aren’t! What do you do instead? A Kruskal-Wallis Test! A Kruskal-Wallis is basically an ANOVA done on the ranked data rather than on the raw data and allows you to compare the groups without needing to meet the assumption of normality.
Example 2: Correlation
Correlation, as I’m sure you’re all aware, is a measure of association. Basically, if you’ve got variables X and Y, correlation is a measure of how much X changes in relation to the changes in Y (or vice-versa). A correlation of 1 suggests that there is a perfect increasing relationship; a correlation of -1 suggests that there is a perfect decreasing relationship.
Scenario: You have a bunch of measurements on two variables. Drug measures the amount of a medicine in a patient’s system. Response measures the amount of some disease marker in the same patient. You want to see if there’s a relationship between the amount of medicine in a patient’s system and the amount of the disease marker present in a patient’s system.
Parametric test: the “usual” correlation, the Pearson Product-Moment Correlation, seems appropriate.
Nonparametric test: The key with the “usual” measure of correlation is that it simply measures the degree of linear association between your variables. If you suspect, for whatever reason, that the relationship between Drug and Response is anything but linear, it’s a good idea to use the Spearman Rank Correlation Coefficient, which is sensitive to non-linear monotonic relationships between variables.
Here, I wanna give you an example of this last one, ‘cause it’s cool. Just as a dumb example, let your sample size be obscenely small (n = 10). Here are your data:
drug response 1 1 2 16 3 81 4 256 5 625 6 1296 7 2401 8 4096 9 6561 10 10000
Notice two things: first, if we plot these two variables, their relationship is clearly nonlinear.

Second, you’ll notice that there is a perfect relationship between drug and response, it’s just not linear. Specifically, Response is just the corresponding Drug value raised to the 4th power, meaning that Response is a perfect monotonic function of Drug! We can easily calculate both Pearson’s and Spearman’s correlations here to see what they’ll say:
Pearson correlation: 0.882
Spearman correlation: 1
Spearman’s picks up on the perfect relationship, but Pearson’s does not! Why? Because it’s not a linear relationship! Pretty cool, huh?
THIS IS WHY YOU ALWAYS PLOT YOUR DATA, DAMMIT.
Side note: Pearson feuded with Spearman over his “adaptation” of Pearson’s beloved correlation coefficient and actually brought the issue in front of the Royal Society for consideration. Oh, you statisticians.
Scrabble Letter Values and the QWERTY Keyboard
Hello everyone and welcome to another edition of “Claudia analyzes crap for no good reason.”
Today’s topic is the relationship between the values of the letters in Scrabble and the frequency of use of the keys on the QWERTY layout keyboard.
This analysis took three main stages:
- Plot the letters of the keyboard by their values in Scrabble.
- Plot the letters of the keyboard by their frequency of use in a semi-long document (~50 pages).
- Compute the correlation between the two and see how strongly they’re related.
Step 1
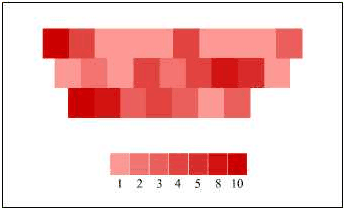
There are 7 categories of letter scores in Scrabble: 1-, 2-, 3-, 4-, 5-, 8-, and 10-point letters. The first thing I decided to do was create gradient to overlay atop a QWERTY and see what the general pattern is. Here is said overlay:
Makes sense. K and J are a little wonky, but that might just be because the fingers on the right hand are meant to be skipping around to all the other more commonly-used letters placed around them. This was the easiest part of the analysis (except for making that stupid gradient; it took a few tries to get the colors at just the right differences for it to be readable but not too varying).
Step 2
I found a 50 or so page Word document of mine that wasn’t on anything specific and broke it down by letter. I put it into Wordle and got this lovely size-based comparison of use:
I then used Wordle’s “word frequency” counter to get the number of times each letter was used. I then ranked the letters by frequency of use.
I took this ranking and compared it to the category breakdown used in Scrabble—that is, since there are 10 letters that are given 1 point each, I took the 10 most frequently used letters in my document and assigned them to group 1, the group that gets a point each. There are 2 letters in Scrabble that get two points each; I took the 11th and 12th most frequently used letters from the document and put them into group 2. I did this for all the letters, down until group 7, the letters that get 10 points each.
So at this point I had a ranking of the frequency of use of letters in an average word document in the same metric as the Scrabble letter breakdown. I made a similar graph overlaying a QWERTY with this data:
Pretty similar to the Scrabble categories, eh? You still get that wonky J thing, too.
Side-by-side comparison:


Step 3
Now comes the fun part! I had two different ways of calculating a correlation.
The first way was the category to category comparison, which would require the use of the Spearman correlation coefficient (used for rank data). Essentially, this correlation would measure how often a letter was placed in the same group (e.g., group 1, group 4) for both the Scrabble ranking and the real data ranking. The Spearman correlation returned was 0.89. Pretty freaking high.
I could also compare the Scrabble categories against the raw frequency data, which would require the use of the polyserial correlation. Since the frequency decreases as the category number increases (group 1 has the highest frequencies, group 10 has the lowest), we would expect some sort of negative correlation. The polyserial correlation returned was -.92. Even higher than the Spearman.
So what can we conclude from this insanity? Basically that there’s a pretty strong correlation between how Scrabble decided to value the letters and the actual frequency of letter use in a regular document. Which is kind of a “duh,” but I like to show it using pretty pictures and stats.
WOO!
Today’s song: Sprawl II (Mountains Beyond Mountains) by Arcade Fire