Correlation and Independence for Multivariate Normal Distributions
OOOOH, thisiscoolthisiscoolthisiscool.
So today in my multivariate class we learned that two sets of variables are independent if and only if they are uncorrelated—but only if the variables come from a bivariate (or higher multivariate dimension) normal distribution. In general, correlation is not enough for independence.
ELABORATION!
Let X be defined as:
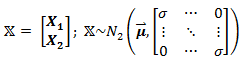
meaning that it is a matrix containing two sets of variables, X1 and X2, and has a bivariate normal distribution. In this case, X1 and X2 are independent, since they are uncorrelated (cov(X1, X2)=cor(X1,X2) = 0, as seen in the off-diagonals of the covariance matrix).
But what happens if X does not have a bivariate distribution? Now let Z ~ N(0,1) (that is, Z follows a standard normal distribution) and define X as:

So before we even do anything, it’s clear that X1 and X2 are dependent, since we can perfectly predict X2 by knowing X1 or vice versa. However, they are uncorrelated:

(The expected value of Z3 is zero, since Z is normal and the third moment, Z3, is skew.)
So why does zero correlation not imply independence, as in the first example? Because X2 is not normally distributed (a squared standard normal variable actually follows the chi-square distribution), and thus X is not bivariate normal!
Sorry, I thought that was cool.
Stats + Primes
So I finished my stats final today. The 3 questions asked resulted in 27 pages of answers, and I think I did pretty well. Here are some things on which we were tested:
- starplots
- biplots
- principle components analysis (PCA)
- exploratory factor analysis (EFA)
- computing the variance of a set of principle component scores (stupid eigenvalues)
- explaining why fitting an EFA model to original data is the same as fitting it to the standardized data
- finding the Fisher direction and standardizing it to unit length, then finding the related Fisher ratio
- finding the value of the Fisher ratio along the first PCA direction
- finding within group variance/covariance matrices
- computing posterior probabilities using the Bayes formula and the normality pdf’s.
Freaking awesome!
I think my favorite’s the non-primes.
