Okay, today’s going to be a quick little blog ‘cause I’m busy trying to organize/transfer/protect from any possible massive hard drive failures my music library. It’s stressing me out.

While I was working on the “References” section of a textbook today at work, I noticed a pattern that I’ve come in contact with several times: there appeared to be a lot more “entries” that started with a letter from the first half of the alphabet (A – M) rather than the latter half (N – Z). I’ve done at least one other analysis regarding this topic, but I decided to do another slightly different one to see if it applied in this case.

QUESTION OF INTEREST
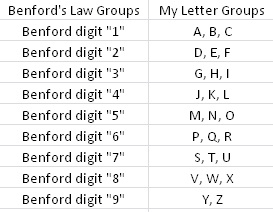
So what is Benford’s Law? For those of you who don’t want to click the link (lazy fools!), Benford’s Law states that with most types of data, the leading digit is a 1 almost one-third of the time, with that probability decreasing as the digit (from 1 to 9) increases. That is, rather than the probability of being a leading digit being equal for each number 1 through 9, the probabilities range from about 30% (for a 1) to about a 4% (for a 9).

What I want to see is this: is there a “Benford’s Law” type phenomenon for the letters of the alphabet? That is, do letters in the first half of the alphabet appear as the first letter of words more often than letters in the latter half of the alphabet?

HYPOTHESIS
In a given set of random words, a greater number of words will start with a letter between A and M than with a letter between N and Z.

METHOD
Using this awesome little utility, I generated (approximately) 5,000 words each from The Bible, Great Expectations, and The Hitchhiker’s Guide to the Galaxy. I then counted how many words there were starting with A, how many words there were starting with B, and so on for each letter of the alphabet.

I then did two other breakdowns of the letters:
A) I divided the alphabet in half (A – M and N – Z) and counted the total number of words for each group.
B) In order to “mirror” a sort of Benford’s Law type of structure, I divided the 26 letters into nine groups (eight groups of three letters each, one group of two letters). I wanted to make a similar breakdown of groups to the nine numbers that Benford’s Law applies to, just to see if that sort of arbitrary screwing around did anything. Visualization ‘cause I suck at explaining stuff when I’m in a hurry:

Kay? Kay.

RESULTS

I made charts!

By letter:

By “half of the alphabet” in what is probably the most worthless visual ever:

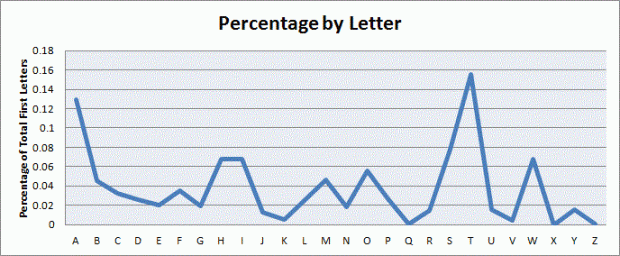
By semi-arbitrary group (dark blue) with Benford’s percentages by number (light blue) for comparison:

DISCUSSION

Well, that whole thing sucked. Okay, so obviously it’s not a perfect pattern match and I didn’t do any stats (I WAS IN A HURRY) to see whether there was any statistical significance or anything, but it was fun to screw around with for an hour or so. I wonder how different the results would be (if at all) if I were to use truly random words from the English language, not just random words selected out of three works of fiction. Perhaps material for a later blog…?

END!