Factorial Factory
BOOSH
As some of the comments say, a number of these could be really useful in understanding/expressing series. Unfortunately, I’ve never heard of any of these being explicitly taught.
Hey How I Tile
So in the division between mathematicians and statisticians, I still firmly place myself in the “statistician” camp, as I feel that I could discuss several statistical topics at a graduate+ level (especially things like regression, SEM, multivariate analysis in general, etc.), but I cannot say the same thing about math.
With that in mind, I enjoy the idea of tessellation to the fullest extent of my understanding of it – which is not that deep.
So when I heard this, I got really excited!
An “einstein” is an aperiodic monotile, which means that it is a single shape tiles the plane but does so without a repeating pattern. Apparently a true one has never been found before this. Check out the link above for a better description than I can give, or watch this interview with one of the co-discoverers, Craig Kaplan.
Cool!
Elliptical
It’s interesting how difficult it is to express such a (visually) simple shape.
THAT’S ALL FOR TODAY, I’M BUSY!
The Recamán Sequence
This is super cool, yo.
O LAWDY, WE CODIN’
This was one of my favorite topics we covered in that Algorithms class I took in my final semester at U of I:
This is such a great explanation of it too. I love the graph.
Bikin’
This is REALLY interesting, yo.
Unless I’m missing it, it’d be nice if they reported the actual correlations visualized on page 5. What is a “good correlation”?
Get The Fact(orials)
Ugh, the Gamma Function.
He is a wild child, but he is extremely cool.
What’s even wilder is that you can actually model some probabilities using this thing.
Isn’t that just…wild?
I love this kind of stuff.
Nummers
Enthusiasm is so important in teaching. That’s one reason why I really like this explanation of why the square root of two is irrational.
I also like how he explains the proofs. They’re simple, but they’re so simple that I think it’s easy to overlook them and their importance.
Yay irrational numbers!
!
I love this kind of stuff. I doubt that anyone who reads this garbage blog is interested enough in this to watch the vid, but it’s fascinating to me.
Also, I’ve never seen integration by parts done the way he does it. Cool!
Sort and the world sorts with you
Hnnnnnn I love sorting algorithms skerthsglhsflasfhsdalfsjdfsa
(flailing)
I posted something very similar to this quite a long time ago, but this one is much more comprehensive. It also had quite a few sorts that I didn’t know about and had to look up (like the circle sort and the grailsort to name two of them).
Check it out! Except if you’re prone to seizures. Then stay away.
Calculus on the Brain
I don’t know what it is about calculus, but every time I’ve had to deal with it, it really gets into my brain.
Like…it permeates my dreams and becomes something that my brain just can’t let go of. I remember this happening the first time I took an actual calculus class during that first summer at UBC (yeah, I know, first calculus class was during grad school. Shut up.). When I went to Boston for the APS conference, all I could think of was calculus. All my brain produced in my dreams was calculus-related.
Same thing now. Now that I’m teaching it, all my brain does is produce calculus-related thoughts and dreams. I’m waking up thinking of limits.
It’s kind of a nice throwback to when I was first learning calc.
And, you know, it always makes me think of Leibniz, so there ya go.
ZoomaZoomaMathsGear
Heyo.
Y’all want some cool math-related stuff? Check out this website.
Favorites:
- Skew dice.
- Shapes of constant width.
- Symmetry groups wrapping paper (I don’t know why, but I love the symmetry groups. I’ve blogged about them a few times.)
- Torus balloons.
- Math stack playing cards.
- RGB/CMYK earrings.
- Galton board (Matt, I think you showed this to me once?)
WOO!
Yo Dawg, I Herd U Like Factorials
Have you ever wondered why zero factorial (0!) equals 1? One of my students sent me a link to this explanation. It’s pretty intuitive when explained this way.
Psst…
…you like mathematicians?
Yeah, you do. Here’s a timeline showing when many major math figures lived and what their main contributions were.
(Leibniz FTW.)
AND SPEAKING OF LEIBNIZ…
CALCULUS!
So this guy, 3Blue1Brown, posts all sorts of math-related videos on YouTube. His series “Essence of Calculus” is really interesting and a good way to get into calc if you’re interested in it but you don’t know quite where to start (or if it’s been a while since you’ve learned it).
Nummers
Yo, this is super interesting. Infinities!!
HIGH FRUCTOSE CORN HERO
Y’all want some cool math stuff?
Of course you do.
Nate was reading a Reddit thread titled “What is the coolest mathematical fact you know of?” The two that were the coolest to me are the following:
An explanation of just how many different ways there are to uniquely shuffle a deck of 52 cards.
Graham’s number. Ridiculous.
Seriously, read these. Numbers are amazing.
Poosers
Holy crapples, this is fantastic.
I think they should have assigned this as required reading to all first-year grad students who had to TA as part of their funding, and then made them re-read it at the beginning of every subsequent year so as not to forget important stuff. It’s also still relevant as an instructor. At least, most of it.
Highlights:
“Many instructors assume that students will read what is handed to them; I think this is incorrect.”
Oh my god, yes. This wasn’t something I ever did as a TA, but as an instructor (both at UI and U of C), I like to take time during the first lecture to actually go over the syllabus and any other important hand-outs. I particularly like to do this in the form of a PowerPoint so that I can really focus on the big things. I think it really helps emphasize what’s important to the students rather than making them wade through a two- or three-page document that includes a little information on every aspect of the class.
“People never learn course material as well as when they have to explain it to others.”
U of C has a thing up here for their 200-level stats classes called “continuous tutorial.” This is kind of like drop-in homework help where a TA staffs a computer lab for an hour, and during that hour students from STAT 213 and STAT 217 can drop in, work on homework, and ask questions of the TA if they have them. During my first continuous tutorial, I botched the hell out of a really simple probability question while helping a student. It wasn’t because I didn’t know how to do that type of problem, but because I hadn’t done that type of problem in quite some time, I blanked on the very simple solution and really confused the student. Brilliant, right? It is super important, both as a TA and as an instructor, to actually work through the homeworks assigned to the students and make sure you know how to do them. Because there’s not a lot of things more embarrassing than blanking on a question covering a subject that you supposedly know well enough to teach to the students.
“To me, motivating means addressing the history, culture, and usefulness of mathematics.”
LAKJSDFLASKFJALKF ASDFYADJFSDJ YES YES YES YES YES YES YES A THOUSAND TIMES YES
If you can put the topic into some sort of “non-computational” context, I think students are apt to be more open to it, approach it with less fear, and maybe even get excited about it. This is such an important idea to me, you have no idea.
Yay.
Well, they WERE two doctors (yeah, I know, stupid joke)
This is super coolio.
Well, at least I’m consistent.
Hey, doods.
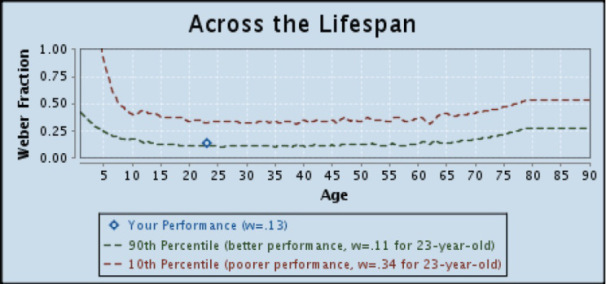
Back in 2012, I took an Approximate Number System aptitude test that I found online.
Then, in 2014, I took it again to see if my score had changed (since I’d done so much more math between 2012 and 2014 than I had prior to 2012). My score didn’t change at all.
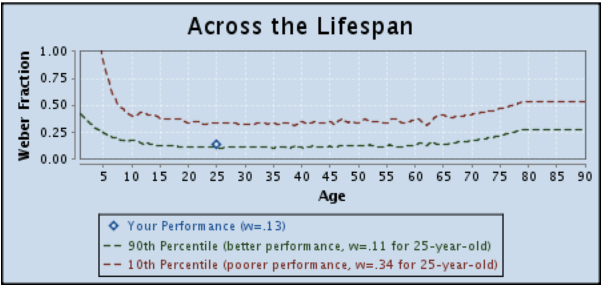
So it’s 2016 now…wanna guess what I did?
I took it again!
And my score is still the same!
2012
2014
2016
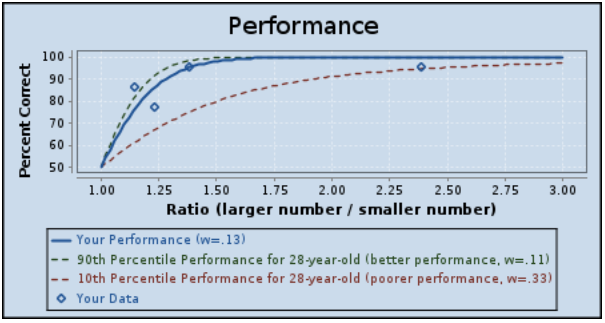
Yeah. I guess the amount of math/numbers I deal with doesn’t affect how good I am at this test. Pretty cool result, though, nonetheless.
Calculus is God
Today I had to go invigilate a MATH 277 final as part of my TA requirements (we each have to invigilate/proctor two final exams; sometimes we get ones we’ve actually been TAs for and sometimes we don’t. This was a case of the latter). It turns out that MATT 277 is University of Calgary’s version of MATH 275, or multivariate calculus. The test involved about 20 or so questions.
Our job as TAs, apart from making everybody sign in on the little attendance sheet, was mainly to just walk around in order to discourage cheating and to help anybody out who raised their hand.
So let me just quickly set the scene for you: a large gym full of 250+ students, a 2-hour exam, and lots and lots of calculus.
I bet you can guess what I was thinking about.
I was thinking about Leibniz!
I was wondering, as I walked down the aisles of seats, watching students write the elongated “s” for integration and the dx/dy (or variations of that) for differentiation, what Leibniz would think if he saw a roomful of people, in 2016, still using some of his original symbols. Like, how ridiculous is that? Calculus has been studied, expanded upon, and extended to a ton of different fields/uses since it was first developed, but we’re still using some of Leibniz’ original symbols.
And what would he think about calculus being taught as basically standard curriculum at universities? What would he think about the tons of different uses of calculus today?
I know I kind of talked about this in a previous post, but I actually think about this quite a bit. Especially today.
Yay calculus! Yay Leibniz!
Baa Baa Black Sheep, Have You Any Blogs?
GUYS I HAVE PURCHASED A SLIDE RULE
Story: Okay, so it’s been like four days since I’ve gone walking, which is four days too many, so I decided to walk down to Chinook Centre (about 13 miles round trip). However, once I got down there, I changed my mind and decided to check out the Value Village close to the mall instead. I was just going to look around since I have practically no money at the moment, but when I was digging through the miscellaneous baskets on one of the shelves I came upon THIS:
And since it was only $2, I had to get it. So I did.
It didn’t have a manual or anything with it and I’ve never used a slide rule before in my life, so I went to teh internetz to see if I could figure out how it works. And it’s super cool! Let me show you a few basic things.
Multiplication: Say I wanted to multiply 1.2 by 3. What I’d do is find 1.2 on the “D” scale and slide my “C” scale so that its 1 is right above 1.2.
Then I would find 3 on my “C” scale. Whatever number on the “D” scale is right below the 3 on the “C” scale is the product of 1.2 times 3: 3.6!
Division: Let’s do 6 divided by 4. You take the divisor, 4, on the “C” scale and set it above the dividend, 6, on the “D” scale like so:
The quotient is whatever number is on the “D” scale right below the 1 on the “C” scale: 1.5!
Finding a square root: Say I wanted to find the square root of 5. I would find 5 on the “A” scale. Whatever number on the “D” scale that is below that 5 is the square root: approximately 2.23!
Super cool. You can also do things like cubes/cube roots, proportions, logarithms, and sines and tangents of angles, but I’m still learning.
WOO!
Mental Math: The Struggle is Real
Alright fools, sit your butts down. Today’s blog post is an important one.
I’ll start this whole thing off with a confession. You’ve all heard me say that I can’t do math in my head, right? Well, that’s a lie. I am perfectly capable of doing math in my head.
I just can’t do it when others expect me to be able to do math in my head.
Elaboration: like a lot of people, I’ve always equated math ability with intelligence. I know that’s a narrow and inaccurate way to define intelligence, but for the longest time, math was my go-to smarts-o-meter. That’s probably because I used to be hella afraid of it and thus considered anyone who wasn’t hella afraid of it to be way smarter than I was.
But anyway.
I’ve long since redefined how I view intelligence. Namely, it’s very obvious to me now that people can easily be “intelligent” in a wide variety of things (think Gardner’s theory of multiple intelligences). A dude who’s fantastic at painting but horrible with numbers, for example, can be just as intelligent as a dude who’s amazing with numbers but not so much with paint. And people who are not “book smart” (or “school smart” or whatever) can be ridiculously intelligent in other aspects of existence that just aren’t captured by that book smartness/school smartness.
I’m sure most if not all of my readers would agree with this.
However, if you’re someone who likes math and are around people who know you like math, they’re probably going to expect you to be good at mental calculations. That’s always been my experience, at least.
And that makes me panic like you wouldn’t believe.
Especially since going into the quantitative/statistics side of things, my ability to do math in my head—“on the fly”—has gotten worse. And I think that’s because if the people I’m around know I’m into stats, I suspect they automatically assume I’m some sort of human calculator. And if I can’t prove my amazing calculating abilities, then I’m too stupid to be studying something like stats. After all, who wants a statistician who can’t add 23 + 27 in their heads?
Here’s the thing. I can add 23 + 27 in my head. It’s super easy to do. But if you just ask me to do it, I will panic and not be able to because I’m too busy freaking out about being judged on if I’m doing the calculation quick enough or what would happen if I make an error.
That sounds really stupid and maybe a bit unclear. Let’s use pictures to clear it up a bit.
Here’s what I would suspect loosely happens in the head of a person without this “math on the fly” anxiety when they’re asked to add 146 + 279:
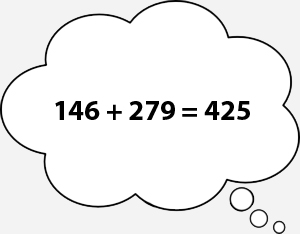
And here’s what happens to me and, I suspect, a good deal of others:
I’m not exaggerating. When someone poses a math question—even something simple like basic addition—I automatically lose focus on the numbers and start freaking out about how dumb they think I am if I don’t answer it right away.
Ridiculous? Yes.
Reality? Yes.
And I can’t be the only one. However, most of my friends (based on just watching them answer impromptu math questions) don’t experience this, so I just wanted to show you how it is for me.
So there you go.
Eigenblogger 